Knödel number

A Knödel number^[1] for a given positive integer n is a composite number m with the property that each i < m coprime to m satisfies 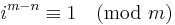$i^{m - n} \equiv 1 \pmod{m}$ . The set of all such integers for n is then called the set of Knödel numbers K_n.

The special case K₁ are the Carmichael numbers.

Examples

n	K_n
1	{561, 1105, 1729, 2465, 2821, 6601, ... }	(sequence A002997 in OEIS)
2	{4, 6, 8, 10, 12, 14, 22, 24, 26, ... }	(sequence A050990 in OEIS)
3	{9, 15, 21, 33, 39, 51, 57, 63, 69, ... }	(sequence A033553 in OEIS)
4	{6, 8, 12, 16, 20, 24, 28, 40, 44, ... }	(sequence A050992 in OEIS)

Literature

Makowski, A (1963). Generalization of Morrow's D-Numbers. p. 71.
Ribenboim, Paulo (1989). The New Book of Prime Number Records. New York: Springer-Verlag. p. 101. ISBN 9780387944579.
Weisstein, Eric W., "Knödel Numbers" from MathWorld.

References

^ Named after Walter Knödel, born May 20th, 1926 in Vienna. Knödel earned a Ph.D. in number theory in 1948 (advisors: Hlawka and Radon) and obtained the habilitation in 1953. Since 1961 he is professor at University of Stuttgart, establishing the new department of computer science, see also [1].